PART 1 OF A FOUR-PART SERIES ON UNDERSTANDING HOW MUCH RESOLUTION A HOLOGRAM NEEDS TO APPEASE THE EYE
I am often asked: “Jon, what is the resolution of a hologram?”
To accurately understand this, one must first understand how to measure the resolution of a standard optical system, as well as the limitations of the human visual system. Only then can you move onto holographic resolution, young Padawan!
This fascinating journey will be made in four parts:
1. theoretical resolving limits modeling the eye as a camera
2. quantifying optical and biological defects that significantly further limit resolution
3. physiological considerations that ultimately impact what you “see”
4. applying all of these factors to the viewing environment to define the resulting perceptual resolution requirements for any display.
We romanticize the eye as the window to the soul, but upon close inspection, that window is rather bleary. So how sharp is our vision really? We begin the trek to ultimate holographic resolution by first understanding the eye as a camera. Turns out it’s not really a very good camera, but more on that in Part 2. Here we will see how we might characterize the human eye as if it were a fine Hasselblad camera – which it is not. Beyond the fact that the principle plane (where incoming light rays converge or diverge) is not in the lens but somewhere in the cornea, or that eye muscles change the shape of the eye to accommodate near or far gazes, or that the eye is constantly twitching to keep the retina from fatiguing, or that the vitreous humor (the goo that fills the eye) has a completely different index of refraction from air - the eye is just like a camera…
The lens of the eye does not work alone since the cornea also provides some of the eye’s focusing power.
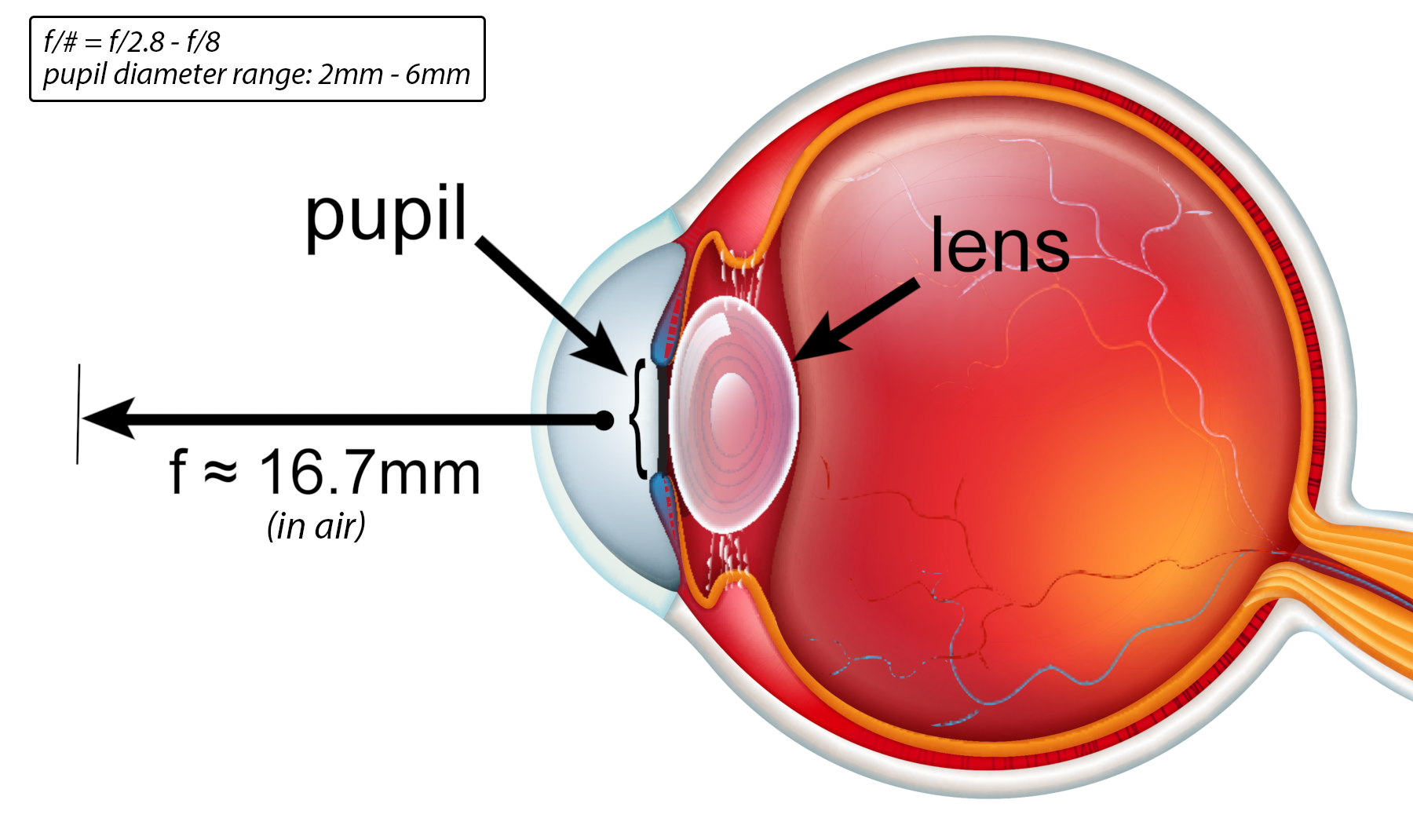
Like a camera, there is a lens assembly to focus the light (lens plus cornea), an aperture (the pupil) to adjust the amount of incoming light, and an image capture surface (the retina). Unlike a camera, the eye does not have a physical or digital shutter since it sends a steady stream of visual information to the brain via the optic nerve. The bandwidth of this optical stream is guesstimated to be equivalent to about 20 million to 200 million bits per second with the retina doing a great deal of pre-processing before images are sent to the brain (for more about how you see with your brain, check out The Evolution of Visual Perception).
We can start assigning camera attributes to the eye using the illustration above. It shows the lens, of course, but we now know that the principle plane is somewhere in the cornea. Some will say that the focal length of the eye is around 22mm; but due to the vitreous humor’s different refractive index from air we must correctly define the focal length of the eye using the refractive index of air to keep the camera metaphor going. This means that to be optically correct we must declare the focal length of the human eye to be ~16.7mm. The pupil is the stand-in for the camera aperture, and its size can range from around 2mm to 8mm. Now that we have the focal length and aperture sizes we can calculate the f-number (f-stop) of our “cranial camera” thusly:
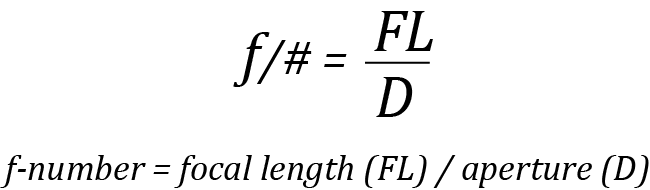
Doing the math with the aperture – I mean pupil – size range of ~2mm – 8mm the focal length of the Hasselblad in our head ranges from ƒ/# ≈ ƒ/2.8 to ƒ/8. Looking these up on a camera spec sheet we would find the ƒ/2.8 camera to have a wide aperture with a shallow depth of field, excellent low-light characteristics, and most suitable for dodging nocturnal predators. At the other extreme, the ƒ/8 camera with its smaller aperture has a very deep depth of field, excellent visibility in broad daylight, and is most suitable for dodging daytime predators.
Because we have two eyes our total horizontal field of view is about 210 degrees allowing us to spot predators sooner.
Now that we have the “camera” defined we can consider the smallest feature this camera can photograph—which turns out to be limited by the laws of physics, specifically diffraction. The illustration here shows an incoming coherent plane wave (i.e. laser light) passing through a surface with a small slit in it. Being coherent, the light waves are both in phase and the same wavelength. As the size of the slit approaches the wavelength of the light the wave passing through it “diffracts” in a spherical pattern to the right and left of the slit due to the wave interfering with itself. Some of the diffracted wave after the slit interferes constructively—meaning that it adds together to form bright spots. Other portions of the diffracted wave interferes destructively—meaning that it cancels itself out forming a dark spot. If a screen is placed at a distance from the slit then the interference pattern may be observable as a series of light and dark bands.

The muscles that move our eyes are the body’s quickest to allow our eyes to dart from point to point almost instantly and faster than any autofocus lens.
Referring to the above interference illustration, if instead of a slit there is a pinhole (i.e. a circular aperture), then instead of vertical bands of interference there would be a bright spot surrounded by rings of interference. This pattern is called an Airy disk after the British astronomer Sir George Biddell Airy, and its size depends on the wavelength of light and the size of the aperture.

This illustration shows the angular radius (θ) of the Airy disk which is from the center of the spot to the center of the first dark ring. This angle is measured in radians which can be calculated from the wavelength and aperture diameter like this:
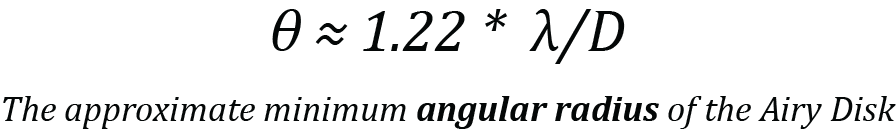
Where λ is the wavelength of the light (in mm) and D is the diameter of the aperture (in mm). This means the larger the aperture, the smaller the Airy disk and the finer the detail that can be resolved (in theory, as you will learn in the next chapter!). Since the Airy disk projects from the hole (aperture) as a cone with a radius angle θ, as the distance to the focal plane increases the Airy disk will necessarily get larger. Keep this in mind for later.
We used coherent light in the diffraction story above because it makes very prominent interference bands, but all light - coherent or not - exhibits interference. Incoherent light such as from the sun or an incandescent bulb has random light wave phases plus a mix of wavelengths that produce interference, but rather than orderly rings they are a jumble of sizes that blur together into a fuzzy spot. Also, we use radians rather than degrees to measure the angle because it simplifies the math and sounds ever so scientific.
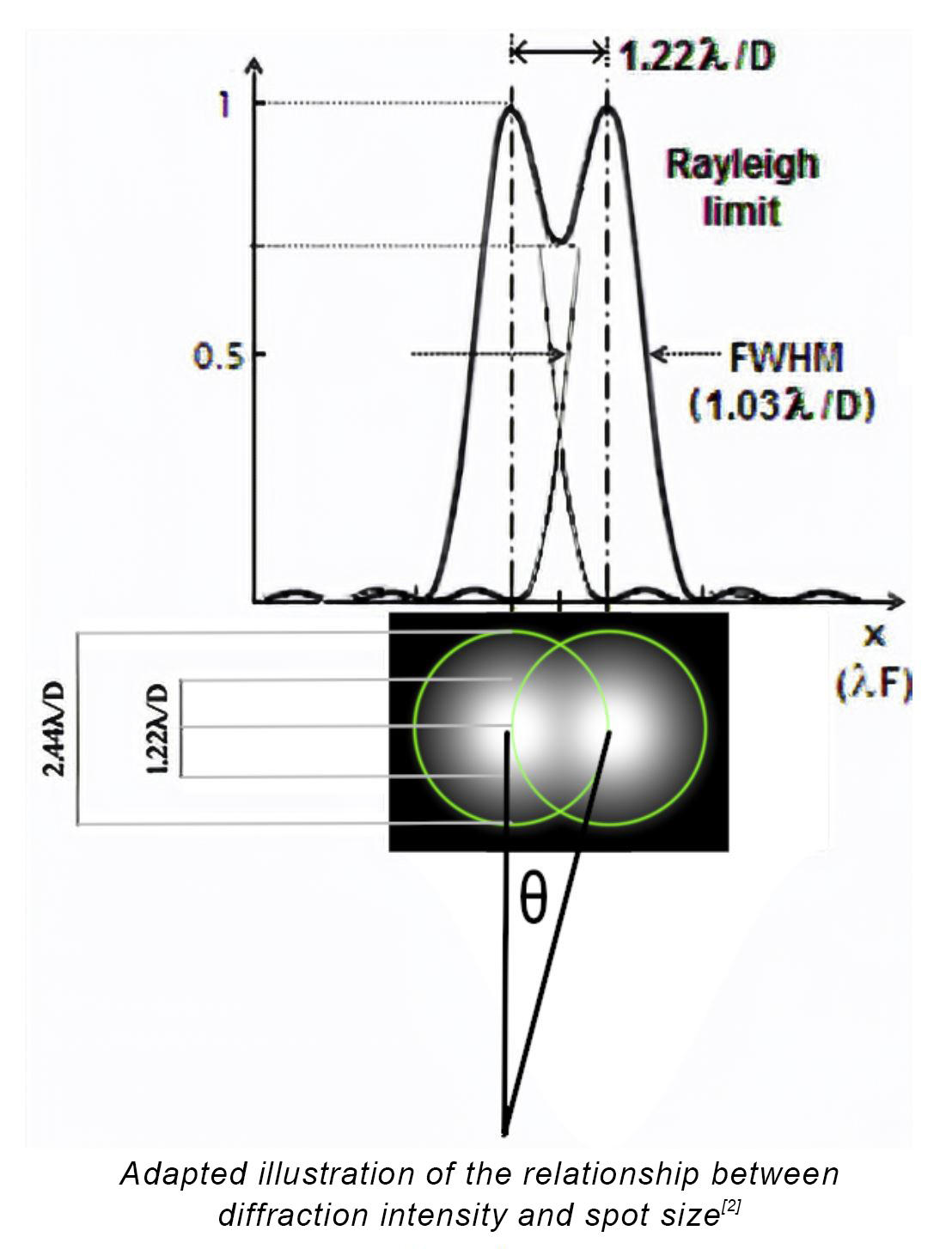
The size of the Airy disk sets a diffraction limit on the resolving power of any optical system simply because if two points get close enough together their Airy disks overlap and they blur together making them indistinguishable. When resolving point pairs (like two stars), the diffraction limit is defined by the Rayleigh Criteria which states that two features are just resolvable when the center of the Airy disc of one coincides with the first minimum (the dark ring) of the other.
Essentially, it defines the limit at which two closely spaced points can be distinguished from one another. It is important to note that the Rayleigh radius (1.22*λ/D) IS the minimum distance between two resolvable spots and not the Airy disk diameter (2.44*λ/D) which is twice this size. This relationship is illustrated here showing two Airy disks overlapping with the green circle outlining the diameter of the disks. The curve above the disks graphs their diffraction intensity.
With 20/20 vision the minimum angular resolution of human vision is about 1 arcminute (0.0167 degrees or 0.0003 radians) which is about 1 mm at 11 feet. A grain of sand is about 1 mm[1].
Earlier we calculated the angular radius of the Airy disk, but to determine the actual size of the radius on the focal plane we must factor in the distance from the aperture (pupil) to the focal plane (retina), otherwise known as the focal length. All we need to do is multiply the angular radius from above by the focal length (FL) like this:
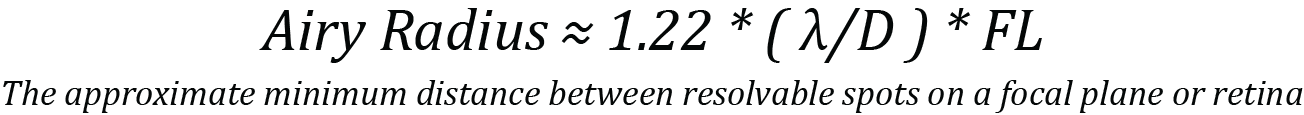
This means that for a given angular radius, the size of the Airy radius depends on the focal length of the optical system. The above equation can be simplified with some algebraic manipulation by using the equation for the f-number (ƒ/# = FL / D) and substituting it in to simplify the equation to this:

This means the resolving power of the eye or any optical system increases as the wavelength decreases (smaller spot size = higher resolving power) or the ƒ/# gets smaller when the aperture (D) gets larger. The Rayleigh Criteria defines how close two targets may be before their Airy disks blur together and the above formula allows us to calculate exactly where that will occur for a given lens ƒ/# and wavelength of light. This becomes the diffraction-limited maximum resolving power of all optical systems including the human eye.
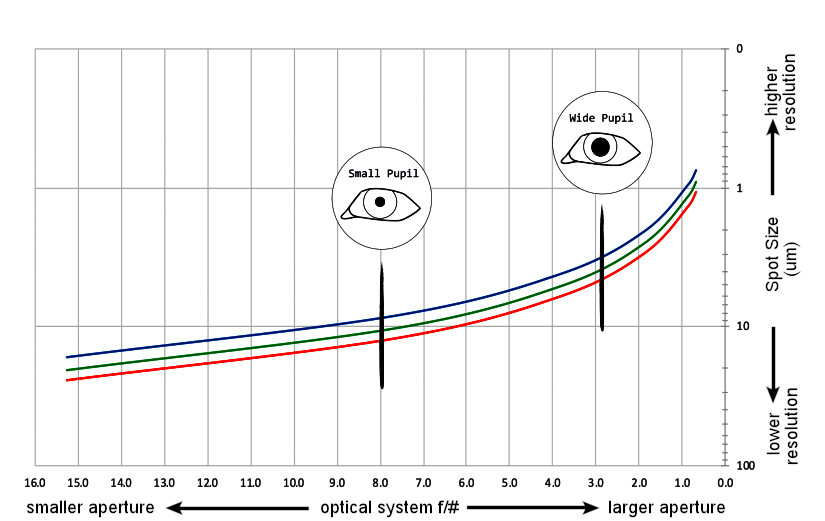
The illustration above shows this relationship between the ƒ/# and maximum diffraction-limited resolving power (Airy disk diameter in μm/cycle) for three wavelengths (red, green, and blue shown respectively). Each wavelength is plotted individually because the wavelength of light affects the spot size a bit differently. The horizontal axis is the ƒ/# with the aperture getting larger towards the right. Note that the range of pupil sizes are highlighted between ƒ/2.8 – ƒ/8. The vertical axis logarithmically plots the spot diameter in um/cycle which gets smaller towards the top indicating higher resolution. The takeaway here is that according only to the Rayleigh diffraction limits, the answer to the question of the smallest detail that the eye can resolve on the retina is between 2 – 12 μm/cycle and are highly dependent on the size of the pupil and wavelength of light.
If we want to know how much resolution any display including holograms will need to satisfy human visual acuity, then as discussed, we first need to establish what the eye is capable of. In Part 1, we granted that the eye is not really a camera, but we considered it as such anyway in order to erect some analytical scaffolding to use for a mathematical analysis of the performance of the human eye. We then found that the laws of physics sets a lower diffraction limit on how small a feature may be resolved due to the Airy disk and the interference of light. This forms the diffraction-limited model of the human eye that we will further build upon in Part 2, where we will add in the myriad of other optical wavefront aberrations suffered by all optical systems including the human eye to see how they (sadly) drag down our visual acuity even further.
Bring your glasses.

[1] Grains of sand can range from between 0.063mm to 2.0mm, depending on the disposition of your beach. [1](#footnotes)
[2] https://www.telescope-optics.net/telescope_resolution.htm#aperture